Het Penrose schaakprobleem opgelost, mat in 1!

De publicatie in de Engelse krant The Telegraph (Sarah Knapton, 14 maart) over de oprichting van het nieuwe Penrose Institute heeft in schaakkringen veel stof doen opwaaien. De beroemde emeritus hoogleraar in de wis- en natuurkunde Roger Penrose, inderdaad de broer van de meermalige Engelse schaakkampioen Jonathan Penrose, haalde een schaakprobleem van stal waarmee hij wil aantonen dat de mens anders en beter denkt dan de computer. Max Pam besteedde er kort aandacht aan in zijn schaakrubriek in Het Parool van afgelopen zaterdag, Frederic Friedel van Chessbase had al eerder uitvoerig gepubliceerd, de Belgische krant De Morgen had het opgepakt en vele andere (lokale) media, schaaksites en sociale media  volgden.

Het nieuwe Penrose Institute (Amerika, Engeland) gaat zich bezighouden met onderzoek naar fundamentele verschillen tussen  kunstmatige en menselijke intelligentie en heeft hiervoor belangrijke sponsors gevonden. Onderzoek naar kunstmatige intelligentie is wereldwijd al een topic. De grote vijf alleen al (Microsoft, Google, Apple, Amazon en Facebook) besteden jaarlijks miljarden dollars aan  onderzoek op dit gebied. Niemand wil hier de slag verliezen.

Roger Penrose presenteerde onderstaande schaakpuzzel, zijn broer zal er ongetwijfeld ook naar hebben gekeken want Penrose beweerde dat het een legale schaakstelling is.

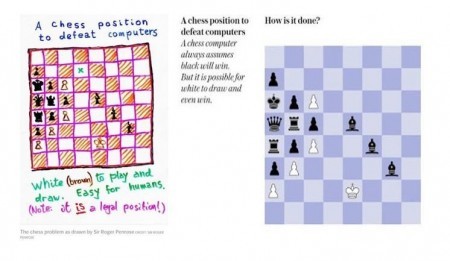
Hij wil nu weten van schakers hoe zij de puzzel hebben opgelost en hoelang zij er over hebben gedaan. Hetzelfde wil hij weten van computers met schaakprogramma’s. Veel programma’s geven volgens hem aan dat zwart groot voordeel heeft in deze stelling. Dit is met name gebaseerd op het aantal stukken van zwart.  Hij overweegt bij mensen die het probleem het snelst hebben opgelost onderzoek te doen met hersenscans om te zien of het denken van de mens ook zichtbaar te maken is in het brein. Dit alles om fundamentele verschillen tussen het denken van mens en machine bloot te leggen. Men wil bewijzen dat het menselijk brein uniek is en blijft.

Drie vragen (wit begint):

1 Kan wit remise houden? Zo ja, hoe dan?

2 Kan wit ook winnen? Zo ja, hoe dan?

( 3 Geef alle zetten die hebben geleid tot deze legale stelling. Dit als extra uitdaging voor de liefhebbers).

Beoordeling van de stelling

Het beoordelen van de stelling is niet moeilijk. Drie lopers is mogelijk door promotie.

Remise lijkt simpel, wit hoeft hier weinig voor te doen. Gewoon op de witte velden blijven met de koning en vooral de zwarte zware stukken en de zwarte koning gevangen houden! Dus niet gaan slaan met de pionnen en ook geen zet doen met de pion op c6.

Wit kan alleen maar winnen als zwart hele domme zetten doet door  alle lopers van de diagonaal b8-h2 te halen en ook weg te blijven van de diagonaal d8-h4. Dan kan de pion promoveren en zelfs een minorpromotie met een loper leidt dan tot mat. Maar we gaan niet uit van domme zetten en winnen is in deze stelling niet realistisch.

Dat computers veel rekenkracht en tijd nodig hebben om alle mogelijkheden na te gaan kunnen we ons  voorstellen met name  door de aanwezigheid van drie lopers. Of programma’s gebaseerd op  kunstmatige intelligentie met gebruik van databases (partijen, probleemstudies en eindspelstudies) beter presteren is niet bekend.  De vraag is zelfs of er al zulke sterke programma’s bestaan?

Out-of-the-box denken

Bij het zien van deze stelling moest ik terugdenken aan een bijeenkomst van midden 70-er jaren van de vorige eeuw met de Engelse arts en psycholoog Edward de Bono (1933). De Bono vergaarde veel bekendheid met Lateral Thinking (lateraal denken) en schreef er  boeken en artikelen over. Hij verzorgde ook lezingen en workshops voor het Nederlandse bedrijfsleven. Tegenwoordig noemen we lateraal denken  out-of-the-box denken!

Bekend is ook zijn methode met de zes gekleurde hoeden. Ik kies hier voor de groene hoed. De groene hoed staat voor innovatie, creativiteit, inventiviteit en nieuwe ideeën.

Door het toepassen hiervan is het in bovenstaande stelling wel mogelijk voor wit om te winnen (mat in 1 te geven zelfs!). Het lijkt flauw, maar is het zeker niet.

Bij de stelling is niet expliciet aangegeven welke spelregels gelden. Iedereen gaat natuurlijk uit van de spelregels van het internationale schaak. Maar waarom zouden er geen andere spelregels van toepassing kunnen zijn? Er zijn veel varianten van het schaakspel en iedere variant heeft eigen regels.

Als we de regels van Crazyhouse of Bughouse toepassen dan blijkt dat we zelfs mat in 1 kunnen geven. Voor Bughouse (in Nederland bekend als doorgeefschaak) bestaat er zelfs een officieel FIDE-reglement met aanvullende spelregels!

Deze oplossing heb ik aan het Penrose Institute voorgelegd en ik ben benieuwd naar hun reactie.

Het Penrose Institute is voornemens de komende maanden meer (schaak)puzzels aan ons voor te leggen in het kader van hun onderzoek. Ik ben benieuwd.