Schaakbreinbrekers
Schaakbreinbrekers

Wilt u uw schaakvaardigheden eens beproeven? Laat eens zien of u de volgende probleempjes het hoofd kunt bieden.
U mag gebruik maken van hulpmiddelen, maar schakel geen andere personen in om u bij te staan. Anders is het niet echt een test van uw hersenen. Schaakpuzzels zijn heilzaam. Hoe groter de mentale uitdaging, des te kleiner de kans op mentaal verval.
1. Tijdens een vriendschappelijk schaakpartijtje is de witte koning per ongeluk van het bord gestoten. Geen van de spelers kan zich herinneren wiens beurt het was of waar de koning stond. Kunt u hen helpen?

Uw oplossing kan pas worden goedgekeurd als u ook kunt aantonen wat de laatste paar zetten moeten zijn geweest.
Kijk aan het einde van dit artikel voor de oplossing.
2. CHESS MATCH

Om het diagram te verduidelijken: wit heeft een koning, een toren, twee lopers en twee pionnen. Zwart heeft alleen nog de koning.
Kijk aan het einde van dit artikel voor de oplossing.
3. Hoeveel vierkanten bevinden zich op het schaakbord?!
Kijk aan het einde van dit artikel voor de oplossing.
4. Na een match om het wereldkampioenschap trad een man brutaalweg naar voren. Hij daagde de tien beste schakers ter wereld uit om het tegen hem op te nemen in een simultaanseance en wilde wedden dat hij minstens vijf punten zou scoren. De regels waren eenvoudig: de tien beste schakers zouden in een cirkel om hem heen geplaatst worden. Ter wille van de eerlijkheid zouden vijf van hen de eerste zet mogen doen, waarop hij op zijn beurt de eerste zet op de overage borden zou doen. Er zou getosst worden om te bepalen welke vijf schakers er zouden beginnen. Er zou gebruik worden gemaakt van een goedgekeurde schaakklok en hij zou niet meer dan dertig seconden per zet mogen gebruiken.
De schaakgrootheden hadden nog nooit van deze man gehoord en waren ervan overtuigd dat hij nooit zo goed kon zijn dat hij ook maar één partij van hen zou winnen. Ze selecteerden de tien sterksten onder hen en bemanden de borden.
Een paar uur later had de man tot ieders verbazing de weddenschap gewonnen.
Hoe was dit mogelijk?
De volgende video laat ons het antwoord zien.
Fragment uit ‘Trick of the mind’, eerste seizoen, eerste episode, uitgezonden in het Verenigd Koninkrijk.
Wat ik me afvraag: is er dan helemaal geen bepaling in de FIDE regels voor het schaakspel opgenomen die een dergelijke truc verbiedt? Wat zou het gevolg zijn als het zwakst geachte team in een teamwedstrijd zich van deze praktijk bedient?
Veel plezier en succes met het oplossen!
Oplossingen
Eerste probleem
Dit was de stelling waar het om begonnen was:

Het is nu duidelijk dat wit 1. c4 moet hebben gespeeld. Het zwarte antwoord was 1. … bxc3 2.Kc3 en dus is c3 het veld waar de witte koning stond, met zwart aan zet!
2. CHESS MATCH

Schaakenthousiasten en anderen die de FIDE regels kennen, zullen gezien hebben dat we een beetje vals gespeeld hebben. Aan het begin van de partij heeft elke speler een wit veld in de rechter benedenhoek. Het is niet onmiddellijk duidelijk aan welke kant de wit- c.q. de zwartspeler gezeten is, maar ongeacht aan welke zijde wit zich bevindt, hij kan een pion tot dame promoveren. Ongeacht aan welke zijde van het bord dat gebeurt, het is mat.
Deze puzzel is afkomstig uit ‘Puzzles, mathematical diversions and brainteasers’ door Erwin Brecher.
3. Hoeveel vierkanten op een schaakbord?
Ofschoon de oplossing niet al te moeilijk is, vergt het een systematische aanpak om tot de juiste oplossing te komen.
Zoals uit de opgave blijkt, worden kinderen uitgedaagd om het juiste aantal vierkanten op het schaakbord te vinden.
Een voor de hand liggend antwoord is 64, maar je kunt je vergissen…
Onderstaand diagram laat inderdaad 64 velden (vierkanten) zien, maar er zijn er nog enkele…

Vergeet het grote vierkant niet (hier rood afgebeeld)…

Ook niet de zestien 2×2 vierkanten die staan afgebeeld (ofschoon dit weer niet de enige 2×2 vierkanten zijn!)…
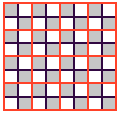
Er zijn nog vele vierkanten met andere afmetingen.
De volledige lijst met antwoorden vind je hieronder
1, 8×8 vierkant
4, 7×7 vierkanten
9, 6×6 vierkanten
16, 5×5 vierkanten
25, 4×4 vierkanten
36, 3×3 vierkanten
49, 2×2 vierkanten
64, 1×1 vierkanten
Zodoende zijn er in werkelijkheid 64 + 49 + 36 + 25 + 16 + 9 + 4 + 1 vierkanten op het schaakbord, dus 204 in totaal.
Voor mijn Engelse versie en het afspelen van de video Klik hier.


